Problem Overview

The HackerRank Jumping on the Clouds problem is a classic algorithmic challenge that tests your ability to make optimal decisions while traversing an array. You are given a series of clouds, represented as an array of integers where 0 indicates a safe cloud and 1 represents a thunderhead that must be avoided. Your task is to start at the first cloud and reach the last one using the minimum number of jumps.

You can jump from your current cloud to either the next cloud or the cloud after that, but you cannot jump onto a cloud marked as 1. The challenge lies in choosing the optimal jumps to minimize the total number while ensuring safety at every step.

The input consists of:

  • An integer n, the total number of clouds.
  • An array of n integers representing the cloud sequence, with 0 for safe and 1 for unsafe clouds.

The output is a single integer representing the minimum number of jumps required to reach the last cloud. This problem emphasizes greedy decision-making, as at each step you need to determine whether a jump of length 1 or 2 leads to fewer total jumps.

Practically, this problem also teaches how to efficiently traverse arrays with conditional logic and highlights the importance of optimizing for minimal operations in algorithms. Solving it improves your understanding of iteration, decision-making under constraints, and applying simple but effective greedy strategies.

Problem Difficulty & Tags

The Jumping on the Clouds problem on HackerRank is considered an Easy-level problem. Despite its simplicity, it is a great exercise for beginners to understand greedy strategies and optimal decision-making.

  • Difficulty: Easy
  • Tags: Arrays, Greedy Algorithms, Iteration, Conditional Logic

This problem is perfect for practicing how to traverse arrays efficiently while making decisions at each step to minimize a certain metric—in this case, the total number of jumps.

Understanding the Problem

The goal of the Jumping on the Clouds problem is to move from the first cloud to the last using the minimum number of jumps while avoiding unsafe clouds (marked as 1). You can jump either one or two clouds ahead, but cannot land on a thunderhead.

Key points to understand:

  • Each cloud is either safe (0) or unsafe (1).
  • You can jump either 1 cloud or 2 clouds forward from your current position.
  • You must avoid landing on unsafe clouds; jumping over them is allowed if possible.
  • The challenge is to minimize the total number of jumps while safely reaching the end.

Essentially, the problem boils down to iterating through the array and making a greedy choice at each step: jump 2 clouds if the second cloud is safe, otherwise jump 1 cloud. This simple logic ensures the minimum jumps while maintaining safety.

Approach / Logic Explanation

To solve the Jumping on the Clouds problem efficiently, I used a greedy approach. The idea is simple: at each step, try to jump 2 clouds if it is safe; otherwise, jump 1 cloud. This ensures the minimum number of jumps to reach the last cloud.

  1. Initialize a counter (jump or total_jump) to zero. This will keep track of the number of jumps made.
  2. Start iterating from the first cloud (i = 0).
  3. While you haven't reached the last cloud:
    • If i + 2 < n and the cloud at i + 2 is safe, jump 2 clouds ahead.
    • Otherwise, jump only 1 cloud ahead.
  4. Increment the jump counter each time you move.
  5. Continue this process until you reach or cross the last cloud.

This approach guarantees a minimal number of jumps and runs in O(n) time with O(1) extra space, as we only maintain a few counters and indices during traversal.

Solution Code

Below are the Python and Java implementations for the Jumping on the Clouds problem. Both solutions follow a greedy approach, trying to jump 2 clouds when possible to minimize the total jumps.

Python Implementation


n = int(input().strip())
c = list(map(int, input().rstrip().split()))
jump = 0
i = 0

while 1:
    if i + 2 < n:
        if c[i + 2] == 0:
            i += 2
        else:
            i += 1
    else:
        break
    jump += 1

if i < n - 1:
    jump += 1

print(jump)

Java Implementation


import java.util.*;
import java.io.*;

class Result {
    public void jumpCloud(int n, int[] ar) {
        int total_jump = 0, i = 0;
        while (true) {
            if (i < n - 2) {
                if (ar[i + 2] == 0) {
                    i += 2;
                } else {
                    i += 1;
                }
                total_jump += 1;
            } else {
                break;
            }
        }
        if (i < n - 1) {
            total_jump++;
        }
        System.out.println(total_jump);
    }
}

public class Solution {
    public static void main(String[] args) {
        InputStreamReader r = new InputStreamReader(System.in);
        BufferedReader br = new BufferedReader(r);
        try {
            int n = Integer.parseInt(br.readLine().trim());
            int[] ar = new int[n + 5];
            StringTokenizer st = new StringTokenizer(br.readLine(), " ");
            for (int i = 0; i < n; i++) {
                ar[i] = Integer.parseInt(st.nextToken());
            }
            Result res = new Result();
            res.jumpCloud(n, ar);
        } catch (Exception ex) {
            ex.printStackTrace();
        }
    }
}

Step-by-Step Walkthrough

Let's break down how the solution works using an example cloud sequence:

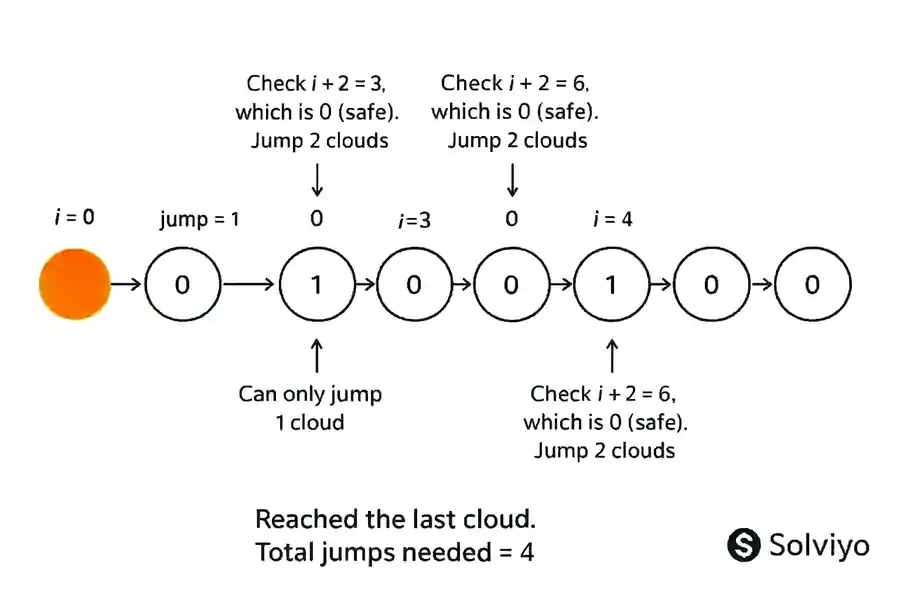
Example Clouds: [0, 0, 1, 0, 0, 1, 0]
  1. Start at the first cloud (i = 0) with jump = 0.
  2. Check if you can jump 2 clouds ahead:
    • Cloud at i + 2 = 2 is 1 (unsafe), so jump only 1 cloud → i = 1.
    Increment jump → jump = 1.
  3. Now at i = 1. Check i + 2 = 3, which is 0 (safe). Jump 2 clouds → i = 3. Increment jump → jump = 2.
  4. At i = 3. Check i + 2 = 5, which is 1 (unsafe). Jump 1 cloud → i = 4. Increment jump → jump = 3.
  5. At i = 4. Check i + 2 = 6, which is 0 (safe). Jump 2 clouds → i = 6. Increment jump → jump = 4.
  6. Reached the last cloud. Total jumps needed = 4.

This demonstrates the greedy approach: always attempt the longest safe jump (2 clouds) to minimize total jumps.

 

Sample Input & Output

Here’s an example to illustrate how the input is processed and the corresponding output:

Input Output Explanation
7
0 0 1 0 0 1 0		 4 Jump sequence: 0 → 1 → 3 → 4 → 6. Total jumps = 4.
6
0 0 0 0 1 0		 3 Jump sequence: 0 → 2 → 3 → 5. Total jumps = 3.
5
0 0 0 0 0		 2 Jump sequence: 0 → 2 → 4. Total jumps = 2.

Time & Space Complexity Analysis

Time Complexity

The solution iterates through the cloud array once, checking whether a jump of length 1 or 2 is possible at each step. For an array of n clouds, this results in a O(n) time complexity. The solution is efficient even for large input sizes since each cloud is visited at most once.

Space Complexity

The solution uses only a few variables such as i and jump to track the current cloud and number of jumps. No additional arrays or data structures proportional to the input size are used, so the space complexity is O(1).

Overall, the approach is both time and space efficient, making it suitable for large-scale input without performance concerns.

Mistakes to Avoid & Tips

Warning: Always check if the next cloud is safe before jumping. Skipping this check can lead to invalid jumps onto unsafe clouds.
Common Error: Trying to modify the array while iterating can cause index errors or skip clouds unintentionally. Simply track the current position and count jumps instead.
Pro Tip: Use a greedy approach by jumping 2 clouds when possible. This ensures the minimum number of jumps in all cases.
Note: If the cloud sequence has consecutive safe clouds, always prioritize jumping 2 clouds to optimize jump count.

Related Problems

If you enjoyed solving Jumping on the Clouds, here are some similar problems that focus on array traversal, greedy algorithms, and minimizing steps:

Conclusion

The Jumping on the Clouds problem is a great exercise for practicing greedy algorithms and understanding how to make optimal decisions while iterating through arrays. By following a simple strategy of jumping 2 clouds whenever possible and 1 cloud otherwise, we can minimize the total number of jumps efficiently.

Key takeaways from this problem:

  • Always consider a greedy approach when trying to minimize or maximize a metric step by step.
  • Pay attention to edge cases, such as consecutive safe clouds or clouds at the end of the array.
  • Keep your solution simple and avoid modifying the input array while iterating.
  • The solution runs in O(n) time and O(1) space, making it efficient for large inputs.

I encourage you to try more greedy algorithm problems on HackerRank to strengthen your problem-solving skills and get comfortable with optimizing both time and space complexity in algorithmic challenges.